通过本实验，掌握Wien电桥正弦振荡器的工作原理、电路调整和测试方法。掌握矩形波振荡器的工作原理、电路调整和测试方法。

一、实验原理

      信号发生器是根据自激振荡原理，使电路在没有外部激励时也能够输出持续稳定的信号波形，信号发生电路包括正弦波形振荡器与非正弦波形振荡器。

      对于正弦波形振荡器，有反馈型振荡器和负阻器件振荡器，后者常用于微波段的振荡。在反馈型振荡器中，根据选频网络的不同，又可分为RC振荡器、LC振荡器、晶体振荡器等。RC振荡器适用于低频振荡，LC振荡器适用于高频振荡，晶体振荡器频率特别稳定。

      对于非正弦波形振荡器，常利用运算放大器作为比较器、或利用数字逻辑门与触发器电路构成的正反馈，产生矩形波、三角波、锯齿波等特殊波形。

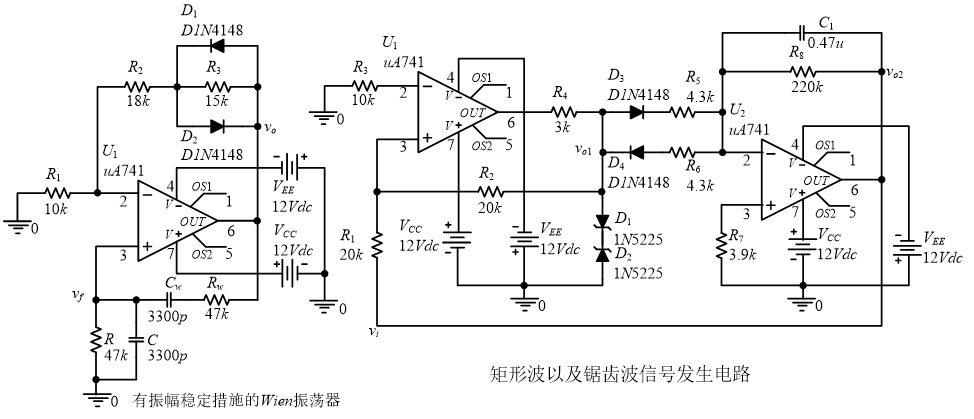
二、实验内容

（一）Wien正弦波振荡器分析

      1、Wien电桥选频网络的交流扫描分析

      对Wien电桥选频网络进行交流扫描分析，观察选频网络的频率特性(幅频与相频)，测量选频网络中心频率f_o、反馈系数F峰值、半功率点频率f_L与f_H，测量0.1f_o、f_L、f_o、f_H、10f_o处的相位值。

      信号源为扫频电压源VAC(0Vdc，1Vac)，重新绘制Wien电桥选频网络原理图。

      仿真设置为AC Sweep/Noise：Logarithmic(Decade)，Start(0.1Hz)，End(10MegHz)，Point/Decade(100)。

      选频网络的幅度频率特性分析变量表达式为V[R:2]/V[R_w:2]。使用标尺可测得中心频率f_o、反馈系数F峰值和半功率频率f_L与f_H。

      选频网络的相位频率特性分析变量表达式为P(V[R:2]/V[R_w:2])。使用标尺可测得0.1f_o、f_L、f_o、f_H、10f_o处的相位值。

      2、幅度平衡条件的分析

      对电路进行瞬态分析，改变系统负反馈通路电阻R₂，以改变振荡器中放大电路的增益，观察放大增益对振荡器能否起振  所产生的影响。测量Wien正弦振荡器的幅度平衡条件。

      仿真设置为Time Domain(Transient)：Run to(50ms)，Start saving data(30ms)，Maximun step(0.02ms)。

      当R₂分别为10kΩ、20kΩ、22kΩ、1GΩ时，记录振荡器输出波形。测量Wien正弦振荡器的幅度平衡条件。

      3、幅度稳定电路的瞬态分析

      对电路进行瞬态分析，改变电阻R₂对振荡器输出峰峰值V_opp的影响。

      仿真设置为Time Domain(Transient)：Run to(24ms)，Start saving data(4ms)，Maximun step(0.02ms)。

      当R₂分别为10kΩ、15kΩ、18kΩ、22kΩ时，记录振荡器输出波形，观察失真情况。

（二）非正弦波振荡器分析

      对电路进行瞬态分析。仿真设置为Time Domain(Transient)：Run to(50ms)，Start saving data(20ms)，Maximun step(0.03ms)。

      1、方波及三角波振荡电路的瞬态分析

      分别测量原电路、仅改变C₁值为0.22μF、仅改变R₂为10kΩ时的方波周期T、占空比τ/T、峰峰值V_opp1以及三角波峰峰值V_opp2。

      2、矩形波及锯齿波振荡电路的瞬态分析

同时将R₅改为1kΩ、R₆改为3.3kΩ，测量矩形波周期T、占空比τ/T、峰峰值V_opp1，锯齿波峰峰值V_opp2。